Расчет параметров уравнения фильтра калмана. Информационный портал по безопасности. Определение сглаживающих свойств
Как то так повелось, что очень нравятся мне всякие алгоритмы, имеющие четкое и логичное математическое обоснование) Но зачастую их описание в интернете настолько перегружено формулами и расчетами, что общий смысл алгоритма понять просто невозможно. А ведь понимание сути и принципа работы устройства/механизма/алгоритма намного важнее, чем заучивание огромных формул. Как это ни банально, но запоминание даже сотни формул ничем не поможет, если не знать, как и где их применить 😉 Собственно, к чему все это.. Решил я замутить описание некоторых алгоритмов, с которыми мне приходилось сталкиваться на практике. Постараюсь не перегружать математическими выкладками, чтобы материал был понятным, а чтение легким.
И сегодня мы поговорим о фильтре Калмана
, разберемся, что это такое, для чего и как он применяется.
Начнем с небольшого примера. Пусть перед нами стоит задача определять координату летящего самолета. Причем, естественно, координата (обозначим ее ) должна определяться максимально точно.
На самолете мы заранее установили датчик, который и дает нам искомые данные о местоположении, но, как и все в этом мире, наш датчик неидеален. Поэтому вместо значения мы получаем:
где – ошибка датчика, то есть случайная величина. Таким образом, из неточных показаний измерительного оборудования мы должны получить значение координаты (), максимально близкое к реальному положению самолета.
Задача поставлена, перейдем к ее решению.
Пусть мы знаем управляющее воздействие (), благодаря которому летит самолет (пилот сообщил нам, какие рычаги он дергает 😉). Тогда, зная координату на k-ом шаге, мы можем получить значение на (k+1) шаге:
Казалось бы, вот оно, то что надо! И никакой фильтр Калмана тут не нужен. Но не все так просто.. В реальности мы не можем учесть все внешние факторы, влияющие на полет, поэтому формула принимает следующий вид:
где – ошибка, вызванная внешним воздействием, неидеальностью двигателя итп.
Итак, что же получается? На шаге (k+1) мы имеем, во-первых, неточное показание датчика , а во-вторых, неточно рассчитанное значение , полученное из значения на предыдущем шаге.
Идея фильтра Калмана заключается в том, чтобы из двух неточных значений (взяв их с разными весовыми коэффициентами) получить точную оценку искомой координаты (для нашего случая). В общем случае, измеряемая величина можем быть абсолютно любой (температура, скорость..). Вот, что получается:
Путем математических вычислений мы можем получить формулу для расчета коэффициента Калмана на каждом шаге, но, как условились в начале статьи, не будем углубляться в вычисления, тем более, что на практике установлено, что коэффициент Калмана с ростом k всегда стремится к определенному значению. Получаем первое упрощение нашей формулы:
А теперь предположим, что связи с пилотом нет, и мы не знаем управляющее воздействие . Казалось бы, в этом случае фильтр Калмана мы использовать не можем, но это не так 😉 Просто “выкидываем” из формулы то, что мы не знаем, тогда
Получаем максимально упрощенную формулу Калмана, которая тем не менее, несмотря на такие “жесткие” упрощения, прекрасно справляется со своей задачей. Если представить результаты графически, то получится примерно следующее:

Если наш датчик очень точный, то естественно весовой коэффициент K должен быть близок к единице. Если же ситуация обратная, то есть датчик у нас не очень хороший, то K должен быть ближе к нулю.
На этом, пожалуй, все, вот так вот просто мы разобрались с алгоритмом фильтрации Калмана! Надеюсь, что статья оказалась полезной и понятной =)
Этот фильтр применяют в разных областях – от радиотехники до экономики. Здесь мы обсудим основную идею, смысл, суть данного фильтра. Излагаться она будет максимально простым языком.
Предположим, что у нас есть необходимость в измерениях некоторых величин некоего объекта. В радиотехнике чаще всего имеют дело с измерениями напряжений на выходе некоего устройства (датчика, антенны и т.д.). В примере с электрокардиографом (см. ) мы имеем дело с измерениями биопотенциалов на теле человека. В экономике, например, измеряемой величиной могут быть курсы валют. Каждыё день курс валют разный, т.е. каждый день “его измерения” дают нам разную величину. А если обобщать, то можно сказать, что большая часть деятельности человека (если не вся) сводится именно к постоянным измерениям-сравнениям тех или иных величин (см. книгу).
Итак, предположим, что мы что-то постоянно измеряем. Так же предположим, что наши измерения всегда идут с некоторой ошибкой – оно и понятно, ведь нет идеальных измерительных приборов, и каждый выдаёт результат с ошибкой. В простейшем случае описанное можно свести к следующему выражению: z=x+y, где x – истинное значение, которое мы хотим измерить и которое измерили бы если бы у нас был идеальный измерительный прибор, y – ошибка измерения, вносимая измерительным прибором, а z – измеренная нами величина. Так вот задача фильтра Калмана состоит в том, чтобы по измеренной нами z всё-таки догадаться (определить), а какое же истинное значение x было, когда мы получали нашу z (в которой "сидит" истинное значение и ошибка измерения). Необходимо отфильтровать (отсеять) из z истинное значение x – убрать из z искажающий шум y. То есть, имея на руках только лишь сумму нам необходимо догадаться о том, какие слагаемые дали эту сумму.
В свете вышеописанного сформулируем теперь всё следующим образом. Пусть есть всего лишь два случайных числа. Нам даётся только их сумма и от нас требуется по этой сумме определить, какими являются слагаемые. Например, нам дали число 12 и говорят: 12 – это сумма чисел x и y, вопрос – чему равны x и y. Чтобы ответить на этот вопрос, составляем уравнение: x+y=12. Мы получили одно уравнение с двумя неизвестными, поэтому, строго говоря, найти два числа которые и дали эту сумму не возможно. Но кое-что об этих числах мы всё-таки можем сказать. Мы можем сказать, что это были либо числа 1 и 11, либо 2 и 10, либо 3 и 9, либо 4 и 8 и т.д., также это либо 13 и -1, либо 14 и -2, либо 15 и -3 и т.д. То есть мы можем по сумме (в нашем примере 12) определить множество возможных вариантов, которые дают в сумме именно 12. Один из этих вариантов – это искомая нами пара, которая на самом деле прямо сейчас и дала 12. Нелишне так же отметить, что все варианты пар чисел дающих в сумме 12 образуют прямую, изображённую на рис.1, которая и задаётся уравнением x+y=12 (y=-x+12).
Рис.1
Таким образом, искомая нами пара лежит где-то на этой прямой. Повторюсь, выбрать из всех этих вариантов ту пару, которая была на самом деле – которая дала число 12, не владея какими-либо дополнительными подсказками, невозможно.
Однако, в ситуации, для которой изобретён фильтр Калмана, такие подсказки есть
. Там заранее о случайных числах кое-что известно. В частности там известна так называемая гистограмма распределения для каждой пары чисел.
Она обычно бывает получена после достаточно длительных наблюдений за выпадениями этих самых случайных чисел.
То есть, например, из опыта известно, что в 5% случаев обычно выпадает пара x=1, y=8 (обозначим эту пару так: (1,8)), в 2% случаев пара x=2, y=3 (2,3), в 1% случаев пара (3,1), в 0.024% случаев пара (11,1) и т.д. Повторюсь, эта гистограмма задана для всех пар
чисел, в том числе и для тех, что образуют в сумме 12.
Таким образом, для каждой пары, что даёт в сумме 12, мы можем сказать, что, например, пара (1, 11) выпадает в 0.8% случаев, пара (2, 10) – в 1% случаев, пара (3, 9) – в 1.5% случаев и т.д.
Таким образом, мы можем по гистограмме определить, в скольких процентах случаев сумма слагаемых пары равна 12. Пусть, например, в 30% случаев сумма даёт 12. А в остальных 70% выпадают остальные пары – это (1,8), (2,3), (3,1) и т.д. – те, что в сумме дают числа отличные от 12.
Причём пусть, например, пара (7,5) выпадает в 27% случаев в то время, как все остальные пары, что дают в сумме 12, выпадают в 0.024%+0.8%+1%+1.5%+…=3% случаев. Итак, по гистограмме мы выяснили, что числа дающие в сумме 12 выпадают в 30% случаев. При этом мы знаем, что если выпало 12, то чаще всего (в 27% из 30%) причиной этого является пара (7,5).
То есть если уже
выпало 12, то мы можем сказать, что в 90% (27% из 30% – или, что то же самое 27 раз из каждых 30-ти) причиной выпадения 12 является пара (7,5). Зная, что чаще всего причиной получения суммы равной 12 является пара (7,5) логично предположить, что, скорее всего, она выпала и сейчас.
Конечно, всё-таки не факт, что на самом деле сейчас число 12 образовано именно этой парой, однако, в следующие разы, если нам попадётся 12, и мы опять предположим пару (7,5), то где-то в 90% случаев из 100% окажемся правы.
А вот если мы будем предполагать пару (2, 10), то окажемся правы лишь в 1% из 30% случаев, что равно 3.33% правильных догадок по сравнению с 90% при предположении пары (7,5). Вот и всё – в этом и состоит смысл алгоритма фильтра Калмана. То есть фильтр Калмана не гарантирует, что не ошибётся в определении слагаемого по сумме, однако он гарантирует, что ошибётся минимальное количество раз (вероятность ошибки будет минимальна), так как использует статистику – гистограмму выпадения пар чисел.
Так же необходимо подчеркнуть, что часто в алгоритме фильтрации Калмана используется так называемая плотность распределения вероятности (ПРВ). Однако необходимо понимать, что смысл там тот же, что и у гистограммы. Более того, гистограмма – это функция, построенная на основе ПРВ и являющаяся её приближением (см., например, ).
В принципе мы эту гистограмму можем изобразить в виде функции двух переменных – то есть в виде некоей поверхности над плоскостью xy. Там, где поверхность выше, там выше и вероятность выпадения соответствующей пары. На рис.2 изображена такая поверхность.

рис.2
Как видно над прямой x+y=12 (которая есть варианты пар дающих в сумме 12) расположены точки поверхности на разной высоте и наибольшая высота у варианта с координатами (7,5). И когда нам встречается сумма равная 12, в 90% случаев причиной появления этой суммы является именно пара (7,5). Т.е. именно эта пара, дающая в сумме 12, имеет наибольшую вероятность появления при условии, что сумма равна 12.
Таким образом, здесь описана идея лежащая в основе фильтра Калмана. Именно на ней и построены всевозможные его модификации – одношаговые, многошаговые рекуррентные и т.д. Для более глубокого изучения фильтра Калмана рекомендую книгу: Ван Трис Г. Теория обнаружения, оценок и модуляции.
p.s. Для того, кто интересуется объяснениями понятий математики что называется "на пальцах" можно посоветовать вот эту книгу и в частности главы из её раздела "Математика" (саму книгу или отдельные главы из неё вы можете приобрести ).
Фильтр Калмана - это, наверное, самый популярный алгоритм фильтрации, используемый во многих областях науки и техники. Благодаря своей простоте и эффективности его можно встретить в GPS-приемниках, обработчиках показаний датчиков, при реализации систем управления и т.д.
Про фильтр Калмана в интернете есть очень много статей и книг (в основном на английском), но у этих статей довольно большой порог вхождения, остается много туманных мест, хотя на самом деле это очень ясный и прозрачный алгоритм. Я попробую рассказать о нем простым языком, с постепенным нарастанием сложности.
Для чего он нужен?
Любой измерительный прибор обладает некоторой погрешностью, на него может оказывать влияние большое количество внешних и внутренних воздействий, что приводит к тому, что информация с него оказывается зашумленной. Чем сильнее зашумлены данные тем сложнее обрабатывать такую информацию.Фильтр - это алгоритм обработки данных, который убирает шумы и лишнюю информацию. В фильтре Калмана есть возможность задать априорную информацию о характере системе, связи переменных и на основании этого строить более точную оценку, но даже в простейшем случае (без ввода априорной информации) он дает отличные результаты.
Рассмотрим простейший пример - предположим нам необходимо контролировать уровень топлива в баке. Для этого в бак устанавливается емкостный датчик, он очень прост в обслуживании, но обладает некоторыми недостатками - например, зависимость от заправляемого топлива (диэлектрическая проницаемость топлива зависит от многих факторов, например, от температуры), большое влияние «болтанки» в баке. В итоге, информация с него представляет типичную «пилу» с приличной амплитудой. Такого рода датчики часто устанавливаются на тяжелой карьерной технике (не смущайтесь объемам бака):
Фильтр Калмана
Немного отвлечемся и познакомимся с самим алгоритмом. Фильтр Калмана использует динамическую модель системы (например, физический закон движения), известные управляющие воздействия и множество последовательных измерений для формирования оптимальной оценки состояния. Алгоритм состоит из двух повторяющихся фаз: предсказание и корректировка. На первом рассчитывается предсказание состояния в следующий момент времени (с учетом неточности их измерения). На втором, новая информация с датчика корректирует предсказанное значение (также с учетом неточности и зашумленности этой информации):Уравнения представлены в матричной форме, если вы не знаете линейную алгебру - ничего страшного, дальше будет упрощенная версия без матриц для случая с одной переменной. В случае с одной переменной матрицы вырождаются в скалярные значения.
Разберемся сначала в обозначениях: подстрочный индекс обозначает момент времени: k - текущий, (k-1) - предыдущий, знак «минус» в верхнем индексе обозначает, что это предсказанное промежуточное значение.
Описание переменных представлены на следующих изображениях:
Можно долго и нудно описывать, что означают все эти таинственные матрицы переходов, но лучше, на мой взгляд, на реальном примере попробовать применить алгоритм - чтобы абстрактные значения обрели реальный смысл.
Опробуем в деле
Вернемся к примеру с датчиком уровня топлива, так как состояние системы представлено одной переменной (объем топлива в баке), то матрицы вырождаются в обычные уравнения:Определение модели процесса
Для того, чтобы применить фильтр, необходимо определить матрицы/значения переменных определяющих динамику системы и измерений F, B и H:F - переменная описывающая динамику системы, в случае с топливом - это может быть коэффициент определяющий расход топлива на холостых оборотах за время дискретизации (время между шагами алгоритма). Однако помимо расхода топлива, существуют ещё и заправки… поэтому для простоты примем эту переменную равную 1 (то есть мы указываем, что предсказываемое значение будет равно предыдущему состоянию).
B - переменная определяющая применение управляющего воздействия. Если бы у нас были дополнительная информация об оборотах двигателя или степени нажатия на педаль акселератора, то этот параметр бы определял как изменится расход топлива за время дискретизации. Так как управляющих воздействий в нашей модели нет (нет информации о них), то принимаем B = 0.
H - матрица определяющая отношение между измерениями и состоянием системы, пока без объяснений примем эту переменную также равную 1.
Определение сглаживающих свойств
R - ошибка измерения может быть определена испытанием измерительных приборов и определением погрешности их измерения.Q - определение шума процесса является более сложной задачей, так как требуется определить дисперсию процесса, что не всегда возможно. В любом случае, можно подобрать этот параметр для обеспечения требуемого уровня фильтрации.
Реализуем в коде
Чтобы развеять оставшиеся непонятности реализуем упрощенный алгоритм на C# (без матриц и управляющего воздействия):class KalmanFilterSimple1D
{
public double X0 {get; private set;} // predicted state
public double P0 { get; private set; } // predicted covariance
Public double F { get; private set; } // factor of real value to previous real value
public double Q { get; private set; } // measurement noise
public double H { get; private set; } // factor of measured value to real value
public double R { get; private set; } // environment noise
Public double State { get; private set; }
public double Covariance { get; private set; }
Public KalmanFilterSimple1D(double q, double r, double f = 1, double h = 1)
{
Q = q;
R = r;
F = f;
H = h;
}
Public void SetState(double state, double covariance)
{
State = state;
Covariance = covariance;
}
Public void Correct(double data)
{
//time update - prediction
X0 = F*State;
P0 = F*Covariance*F + Q;
//measurement update - correction
var K = H*P0/(H*P0*H + R);
State = X0 + K*(data - H*X0);
Covariance = (1 - K*H)*F;
}
}
// Применение...
Var fuelData = GetData();
var filtered = new List();
Var kalman = new KalmanFilterSimple1D(f: 1, h: 1, q: 2, r: 15); // задаем F, H, Q и R
kalman.SetState(fuelData, 0.1); // Задаем начальные значение State и Covariance
foreach(var d in fuelData)
{
kalman.Correct(d); // Применяем алгоритм
Filtered.Add(kalman.State); // Сохраняем текущее состояние
}
Результат фильтрации с данными параметрами представлен на рисунке (для настройки степени сглаживания - можно изменять параметры Q и R):
За рамками статьи осталось самое интересное - применение фильтра Калмана для нескольких переменных, задание взаимосвязи между ними и автоматический вывод значений для ненаблюдаемых переменных. Постараюсь продолжить тему как только появится время.
Надеюсь описание получилось не сильно утомительным и сложным, если остались вопросы и уточнения - добро пожаловать в комментарии)
Винеровские фильтры лучше всего подходят для обработки процессов или отрезков процессов в целом (блочная обработка). Для последовательной обработки требуется текущая оценка сигнала на каждом такте с учетом информации, поступающей на вход фильтра в процессе наблюдения.
При винеровской фильтрации каждый новый отсчет сигнала потребовал бы пересчета всех весовых коэффициентов фильтра. В настоящее время широкое распространение получили адаптивные фильтры, в которых поступающая новая информация используется для непрерывной корректировки ранее сделанной оценки сигнала (сопровождение цели в радиолокации, системы автоматического регулирования в управлении и т.д). Особенный интерес представляют адаптивные фильтры рекурсивного типа, известные как фильтр Калмана.
Эти фильтры широко используются в контурах управления в системах автоматического регулирования и управления. Именно оттуда они и появились, подтверждением чему служит столь специфическая терминология, используемая при описании их работы, как пространство состояний.
Одна из основных задач, требующих своего решения в практике нейронных вычислений, – получение быстрых и надежных алгоритмов обучения НС. В этой связи может оказаться полезным использование в контуре обратной связи обучающего алгоритма линейных фильтров. Так как обучающие алгоритмы имеют итеративную природу, такой фильтр должен представлять собой последовательное рекурсивное устройство оценки.
Задача оценки параметров
Одной из задач теории статистических решений, имеющих большое практическое значение, является задача оценки векторов состояния и параметров систем, которая формулируется следующим образом. Предположим, необходимо оценить значение векторного параметра $X$, недоступного непосредственному измерению. Вместо этого измеряется другой параметр $Z$, зависящий от $X$. Задача оценивания состоит в ответе на вопрос: что можно сказать об $X$, зная $Z$. В общем случае, процедура оптимальной оценки вектора $X$ зависит от принятого критерия качества оценки.
Например, байесовский подход к задаче оценки параметров требует полной априорной информации о вероятностных свойствах оцениваемого параметра, что зачастую невозможно. В этих случаях прибегают к методу наименьших квадратов (МНК), который требует значительно меньше априорной информации.
Рассмотрим применения МНК для случая, когда вектор наблюдения $Z$ связан с вектором оценки параметров $X$ линейной моделью, и в наблюдении присутствует помеха $V$, некоррелированная с оцениваемым параметром:
$Z = HX + V$, (1)
где $H$ – матрица преобразования, описывающая связь наблюдаемых величин с оцениваемыми параметрами.
Оценка $X$, минимизирующая квадрат ошибки, записывается следующим образом:
$X_{оц}=(H^TR_V^{-1}H)^{-1}H^TR_V^{-1}Z$, (2)
Пусть помеха $V$ не коррелирована, в этом случае матрица $R_V$ есть просто единичная матрица, и уравнение для оценки становится проще:
$X_{оц}=(H^TH)^{-1}H^TZ$, (3)
Запись в матричной форме сильно экономит бумагу, но может быть для кого то непривычна. Следующий пример, взятый из монографии Коршунова Ю. М. "Математические основы кибернетики", все это иллюстрирует.
Имеется следующая электрическая цепь:
Наблюдаемые величины в данном случае – показания приборов $A_1 = 1 A, A_2 = 2 A, V = 20 B$.
Кроме того, известно сопротивление $R = 5$ Ом. Требуется оценить наилучшим образом, с точки зрения критерия минимума среднего квадрата ошибки значения токов $I_1$ и $I_2$. Самое важное здесь заключается в том, что между наблюдаемыми величинами (показаниями приборов) и оцениваемыми параметрами существует некоторая связь. И эта информация привносится извне.
В данном случае, это законы Кирхгофа, в случае фильтрации (о чем речь пойдет дальше) – авторегрессионная модель временного ряда, предполагающая зависимость текущего значения от предшествующих.
Итак, знание законов Кирхгофа, никак не связанное с теорией статистических решений, позволяет установить связь между наблюдаемыми значениями и оцениваемыми параметрами (кто изучал электротехнику – могут проверить, остальным придется поверить на слово):
$$z_1 = A_1 = I_1 + \xi_1 = 1$$
$$z_2 = A_2 = I_1 + I_2 + \xi_2 = 2$$
$$z_2 = V/R = I_1 + 2 * I_2 + \xi_3 = 4$$
Это же в векторной форме:
$$\begin{vmatrix} z_1\\ z_2\\ z_3 \end{vmatrix} = \begin{vmatrix} 1 & 0\\ 1 & 1\\ 1 & 2 \end{vmatrix} \begin{vmatrix} I_1\\ I_2 \end{vmatrix} + \begin{vmatrix} \xi_1\\ \xi_2\\ \xi_3 \end{vmatrix}$$
Или $Z = HX + V$, где
$$Z= \begin{vmatrix} z_1\\ z_2\\ z_3 \end{vmatrix} = \begin{vmatrix} 1\\ 2\\ 4 \end{vmatrix} ; H= \begin{vmatrix} 1 & 0\\ 1 & 1\\ 1 & 2 \end{vmatrix} ; X= \begin{vmatrix} I_1\\ I_2 \end{vmatrix} ; V= \begin{vmatrix} \xi_1\\ \xi_2\\ \xi_3 \end{vmatrix}$$
Считая значения помехи некоррелированными между собой, найдем оценку I 1 и I 2 по методу наименьших квадратов в соответствии с формулой 3:
$H^TH= \begin{vmatrix} 1 & 1& 1\\ 0 & 1& 2 \end{vmatrix} \begin{vmatrix} 1 & 0\\ 1 & 1\\ 1 & 2 \end{vmatrix} = \begin{vmatrix} 3 & 3\\ 3 & 5 \end{vmatrix} ; (H^TH)^{-1}= \frac{1}{6} \begin{vmatrix} 5 & -3\\ -3 & 3 \end{vmatrix} $;
$H^TZ= \begin{vmatrix} 1 & 1& 1\\ 0 & 1& 2 \end{vmatrix} \begin{vmatrix} 1 \\ 2\\ 4 \end{vmatrix} = \begin{vmatrix} 7\\ 10 \end{vmatrix} ; X{оц}= \frac{1}{6} \begin{vmatrix} 5 & -3\\ -3 & 3 \end{vmatrix} \begin{vmatrix} 7\\ 10 \end{vmatrix} = \frac{1}{6} \begin{vmatrix} 5\\ 9 \end{vmatrix}$;
Итак $I_1 = 5/6 = 0,833 A$; $I_2 = 9/6 = 1,5 A$.
Задача фильтрации
В отличие от задачи оценки параметров, которые имеют фиксированные значения, в задаче фильтрации требуется оценивать процессы, то есть находить текущие оценки изменяющегося во времени сигнала, искаженного помехой, и, в силу этого, недоступного непосредственному измерению. В общем случае вид алгоритмов фильтрации зависит от статистических свойств сигнала и помехи.
Будем предполагать, что полезный сигнал – медленно меняющаяся функция времени, а помеха – некоррелированный шум. Будем использовать метод наименьших квадратов, опять же по причине отсутствия априорных сведений о вероятностных характеристиках сигнала и помехи.
Вначале получим оценку текущего значения $x_n$ по имеющимся $k$ последним значениям временного ряда $z_n, z_{n-1},z_{n-2}\dots z_{n-(k-1)}$. Модель наблюдения та же, что и в задаче оценки параметров:
Понятно, что $Z$ – это вектор–столбец, состоящий из наблюдаемых значений временного ряда $z_n, z_{n-1},z_{n-2}\dots z_{n-(k-1)}$, $V$ – вектор–столбец помехи $\xi _n, \xi _{n-1},\xi_{n-2}\dots \xi_{n-(k-1)}$, искажающий истинный сигнал. А что означают символы $H$ и $X$? О каком, например, векторе–столбце $X$ может идти речь, если все, что необходимо, – это дать оценку текущего значения временного ряда? А что понимать под матрицей преобразований $H$, вообще непонятно.
На все эти вопросы можно ответить только при условии введения в рассмотрение понятия модели генерации сигнала. То есть, необходима некоторая модель исходного сигнала. Это и понятно, при отсутствии априорной информации о вероятностных характеристиках сигнала и помехи остается только строить предположения. Можно назвать это гаданием на кофейной гуще, но специалисты предпочитают другую терминологию. На их "фене" это называется параметрическая модель.
В данном случае оцениваются параметры именно этой модели. При выборе подходящей модели генерации сигнала вспомним о том, что любую аналитическую функцию можно разложить в ряд Тейлора. Поразительное свойство ряда Тейлора заключается в том, что форма функции на любом конечном расстоянии $t$ от некой точки $x=a$ однозначно определяется поведением функции в бесконечно малой окрестности точки $x=a$ (речь идет о ее производных первого и высшего порядков).
Таким образом, существование рядов Тейлора означает, что аналитическая функция обладает внутренней структурой с очень сильной связью. Если, например, ограничиться тремя членами ряда Тейлора, то модель генерации сигнала будет выглядеть так:
$x_{n-i} = F_{-i}x_n$, (4)
$$X_n= \begin{vmatrix} x_n\\ x"_n\\ x""_n \end{vmatrix} ; F_{-i}= \begin{vmatrix} 1 & -i & i^2/2\\ 0 & 1 & -i\\ 0 & 0 & 1 \end{vmatrix} $$
То есть формула 4, при заданном порядке полинома (в примере он равен 2) устанавливает связь между $n$-ым значением сигнала во временной последовательности и $(n-i)$–ым. Таким образом, оцениваемый вектор состояния в данном случае включает в себя, помимо собственно оцениваемого значения, первую и вторую производную сигнала.
В теории автоматического управления такой фильтр назвали бы фильтром с астатизмом 2-го порядка. Матрица преобразования $H$ для данного случая (оценка осуществляется по текущему и $k-1$ предшествующим выборкам) выглядит так:
$$H= \begin{vmatrix} 1 & -k & k^2/2\\ - & - & -\\ 1 & -2 & 2\\ 1 & -1 & 0.5\\ 1 & 0 & 0 \end{vmatrix}$$
Все эти числа получаются из ряда Тейлора в предположении, что временной интервал между соседними наблюдаемыми значениями постоянный и равен 1.
Итак, задача фильтрации при принятых нами предположениях свелась к задаче оценки параметров; в данном случае оцениваются параметры принятой нами модели генерации сигнала. И оценка значений вектора состояния $X$ осуществляется по той же формуле 3:
$$X_{оц}=(H^TH)^{-1}H^TZ$$
По сути, мы реализовали процесс параметрического оценивания, основанный на авторегрессионной модели процесса генерации сигнала.
Формула 3 легко реализуется программно, для этого нужно заполнить матрицу $H$ и вектор столбец наблюдений $Z$. Такие фильтры называются фильтры с конечной памятью , так как для получения текущей оценки $X_{nоц}$ они используют последние $k$ наблюдений. На каждом новом такте наблюдения к текущей совокупности наблюдений прибавляется новое и отбрасывается старое. Такой процесс получения оценок получил название скользящего окна .
Фильтры с растущей памятью
Фильтры с конечной памятью обладают тем основным недостатком, что после каждого нового наблюдения необходимо заново производить полный пересчет по всем хранящимся в памяти данным. Кроме того, вычисление оценок можно начинать только после того, как накоплены результаты первых $k$ наблюдений. То есть эти фильтры обладают большой длительностью переходного процесса.
Чтобы бороться с этим недостатком, необходимо перейти от фильтра с постоянной памятью к фильтру с растущей памятью . В таком фильтре число наблюдаемых значений, по которым производится оценка, должна совпадать с номером n текущего наблюдения. Это позволяет получать оценки, начиная с числа наблюдений, равного числу компонент оцениваемого вектора $X$. А это определяется порядком принятой модели, то есть сколько членов из ряда Тейлора используется в модели.
При этом с ростом n улучшаются сглаживающие свойства фильтра, то есть повышается точность оценок. Однако непосредственная реализация этого подхода связана с возрастанием вычислительных затрат. Поэтому фильтры с растущей памятью реализуются как рекуррентные .
Дело в том, что к моменту n мы уже имеем оценку $X_{(n-1)оц}$, в которой содержится информация обо всех предыдущих наблюдениях $z_n, z_{n-1}, z_{n-2} \dots z_{n-(k-1)}$. Оценку $X_{nоц}$ получаем по очередному наблюдению $z_n$ с использованием информации, хранящейся в оценке $X_{(n-1)}{\mbox {оц}}$. Такая процедура получила название рекуррентной фильтрации и состоит в следующем:
- по оценке $X_{(n-1)}{\mbox {оц}}$ прогнозируют оценку $X_n$ по формуле 4 при $i = 1$: $X_{\mbox {nоцаприори}} = F_1X_{(n-1)оц}$. Это априорная оценка;
- по результатам текущего наблюдения $z_n$, эту априорную оценку превращают в истинную, то есть апостериорную;
- эта процедура повторяется на каждом шаге, начиная с $r+1$, где $r$ – порядок фильтра.
Окончательная формула рекуррентной фильтрации выглядит так:
$X_{(n-1)оц} = X_{\mbox {nоцаприори}} + (H^T_nH_n)^{-1}h^T_0(z_n - h_0 X_{\mbox {nоцаприори}})$, (6)
где для нашего фильтра второго порядка:
Фильтр с растущей памятью, работающий в соответствии с формулой 6 – частный случай алгоритма фильтрации, известного под названием фильтра Калмана.
При практической реализации этой формулы необходимо помнить, что входящая в него априорная оценка определяется по формуле 4, а величина $h_0 X_{\mbox {nоцаприори}}$ представляет собой первую компоненту вектора $X_{\mbox {nоцаприори}}$.
У фильтра с растущей памятью имеется одна важная особенность. Если посмотреть на формулу 6, то окончательная оценка есть сумма прогнозируемого вектора оценки и корректирующего члена. Эта поправка велика при малых $n$ и уменьшается при увеличении $n$, стремясь к нулю при $n \rightarrow \infty$. То есть с ростом n сглаживающие свойства фильтра растут и начинает доминировать модель, заложенная в нем. Но реальный сигнал может соответствовать модели лишь на отдельных участках, поэтому точность прогноза ухудшается.
Чтобы с этим бороться, начиная с некоторого $n$, накладывают запрет на дальнейшее уменьшение поправочного члена. Это эквивалентно изменению полосы фильтра, то есть при малых n фильтр более широкополосен (менее инерционен), при больших – он становится более инерционен.
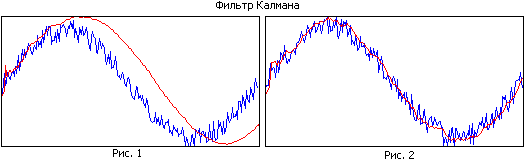
Сравните рисунок 1 и рисунок 2. На первом рисунке фильтр имеет большую память, при этом он хорошо сглаживает, но в силу узкополосности оцениваемая траектория отстает от реальной. На втором рисунке память фильтра меньше, он хуже сглаживает, но лучше отслеживает реальную траекторию.
Литература
- Ю.М.Коршунов "Математические основы кибернетики"
- А.В.Балакришнан "Теория фильтрации Калмана"
- В.Н.Фомин "Рекуррентное оценивание и адаптивная фильтрация"
- К.Ф.Н.Коуэн, П.М. Грант "Адаптивные фильтры"
Проведено исследование использования фильтра Калмана в современных разработках комплексированных навигационных систем. Приведен и разобран пример построения математической модели, использующей расширенный фильтр Калмана для повышения точности определения координат беспилотных летательных аппаратов. Рассмотрен частичный фильтр. Сделан краткий обзор научных работ, использующих данный фильтр для повышения надежности и отказоустойчивости навигационных систем. Данная статья позволяет сделать вывод, что использование фильтра Калмана в системах определения местоположения БПЛА практикуется во многих современных разработках. Существует огромное количество вариаций и аспектов такого использования, которое дает и ощутимые результаты в повышении точности, особенно в случае отказа стандартных спутниковых навигационных систем. Это является главным фактором влияния данной технологии на различные научные области, связанные с разработкой точных и отказоустойчивых навигационных систем для различных летательных аппаратов.
фильтр Калмана
навигация
беспилотный летательный аппарат (БПЛА)
1. Макаренко Г.К., Алешечкин А.М. Исследование алгоритма фильтрации при определении координат объекта по сигналам спутниковых радионавигационных систем // Доклады ТУСУРа. – 2012. – № 2 (26). – С. 15-18.
2. Bar-Shalom Y., Li X. R., Kirubarajan T. Estimation with Applications
to Tracking and Navigation // Theory Algorithms and Software. – 2001. – Vol. 3. – P. 10-20.
3. Bassem I.S. Vision based Navigation (VBN) of Unmanned Aerial Vehicles (UAV) // UNIVERSITY OF CALGARY. – 2012. – Vol. 1. – P. 100-127.
4. Conte G., Doherty P. An Integrated UAV Navigation System Based on Aerial Image Matching // Aerospace Conference. – 2008. –Vol. 1. – P. 3142-3151.
5. Guoqiang M., Drake S., Anderson B. Design of an extended kalman filter for uav localization // In Information, Decision and Control. – 2007. – Vol. 7. – P. 224–229.
6. Ponda S.S Trajectory Optimization for Target Localization Using Small Unmanned Aerial Vehicles // Massachusetts institute of technology. – 2008. – Vol. 1. – P. 64-70.
7. Wang J., Garrat M., Lambert A. Integration of gps/ins/vision sensors to navigate unmanned aerial vehicles // IAPRS&SIS. – 2008. – Vol. 37. – P. 963-969.
Одной из актуальных задач современной навигации беспилотных летательных аппаратов (БПЛА) является задача повышения точности определения координат. Эта задача решается путём использования различных вариантов комплексирования навигационных систем. Одним из современных вариантов комплексирования является сочетание gps/глонасс-навигации с расширенным фильтром Калмана (Extended Kalmanfilter), рекурсивно оценивающего точность с помощью неполных и зашумленных измерений. В данный момент существуют и разрабатываются различные вариации расширенного фильтра Калмана, включающие разнообразное число переменных состояний . В этой работе мы покажем, насколько эффективным может быть его использование в современных разработках. Рассмотрим одно из характерных представлений подобного фильтра .
Построение математической модели
В данном примере мы будем говорить только о движении БПЛА в горизонтальной плоскости, иначе, мы рассмотрим так называемую проблему 2d локализации . В нашем случае это оправдано тем, что для многих практически встречающихся ситуаций БПЛА может оставаться примерно на одной и той же высоте. Это предположение широко используется для упрощения моделирования динамики летательных аппаратов . Динамическая модель БПЛА задается следующей системой уравнений:
где {} - координаты БПЛА в горизонтальной плоскости как функции времени, направление БПЛА, угловая скорость БПЛА, и vпутевая скорость БПЛА, функции и будем считать постоянными. Они взаимно независимы, с известными ковариациями![]() и , равными и соответственно и используются для моделирования изменений ускорения БПЛА, вызванных ветром, маневрами пилота и т.д. Значения и являются производными от максимальной угловой скорости БПЛА и опытных значений изменений линейной скорости БЛА, - символ Кронекера.
и , равными и соответственно и используются для моделирования изменений ускорения БПЛА, вызванных ветром, маневрами пилота и т.д. Значения и являются производными от максимальной угловой скорости БПЛА и опытных значений изменений линейной скорости БЛА, - символ Кронекера.
Данная система уравнений будет приближенной из-за нелинейности в модели и из-за присутствия шума. Самый простой способ аппроксимации в данном случае - это приближение методом Эйлера. Дискретная модель динамической системы движения БПЛА показана ниже.
![]()
дискретный вектор состояний фильтра Калмана, позволяющий аппроксимировать значение непрерывного вектора состояний. ∆ - временной интервал между k и k+1 измерениями. {} и {} - последовательности значений белого гауссовского шума с нулевым средним значением. Матрица ковариации для первой последовательности:
Аналогично, для второй последовательности:
Выполнив соответствующие замены в уравнениях системы (2), получаем:
Последовательности и взаимно независимы. Они также являются последовательностями белого гауссовского шума с нулевым средним значением и с матрицами ковариации и соответственно. Преимущество этой формы в том, что она показывает изменение дискретного шума в интервале между каждыми измерениями. В итоге получаем следующую дискретную динамическую модель:
 (3)
(3)
Уравнение для :
= ![]() + , (4)
+ , (4)
где, х и y - координаты БПЛА в k-момент времени, а гауссовская последовательность случайных параметров с нулевым средним значением, которая используется для задания погрешности. Предполагается, что эта последовательность не зависит от {} и {}.
Выражения (3) и (4) служат основой для оценки местоположения БПЛА, где к-е координаты получены с помощью расширенного фильтра Калмана. Моделлирование отказа навигационных систем применительно к данному типу фильтра показывает его существенную эффективность .
Для большей наглядности приведем небольшой простой пример. Пусть некоторый БПЛА летит равноускоренно, с некоторым постоянным ускорением а.
Где, х - координата БПЛА в t-момент времени, а δ - некоторая случайная величина.
Предположим, что у нас есть gps-сенсор, который получает данные о местоположении летательного аппарата. Представим результат моделирования данного процесса в программном пакете MATLAB.

Рис. 1. Фильтрация показания сенсора с помощью фильтра Калмана
На рис. 1 видно, насколько эффективным может быть использование фильтрации по алгоритму Калмана.
Однако в реальной ситуации сигналы зачастую имеют нелинейную динамику и ненормальный шум. Именно в таких случаях и используется расширенный фильтр Калмана. В том случае, если дисперсии шумов не слишком велики (т.е. линейная аппроксимация является адекватной), применение расширенного фильтра Калмана дает решение задачи с высокой точностью. Однако в том случае, когда шумы не являются гауссовскими, расширенный фильтр Калмана применять нельзя. В этом случае обычно применяют частичный фильтр, в котором используются численные методы взятия интегралов на основе методов Монте Карло с марковскими цепями.
Частичный фильтр
Представим один из алгоритмов, развивающих идеи расширенного фильтра Калмана - частичный фильтр. Частичная фильтрация является неоптимальным способом фильтрации, который работает при выполнении объединения методом Монте-Карло на множестве частиц, которые представляют собой распределение вероятностей процесса. Здесь частица это элемент, взятый из априорного распределения оцениваемого параметра. Основная идея частичного фильтра заключается в том, что большое количество частиц может быть использовано для представления оценки распределения. Чем большее число частиц используется, тем точнее множество частиц будет представлять априорное распределение. Фильтр частиц инициализируется помещением в него N частиц из априорного распределения параметров, которые мы хотим оценить. Алгоритм фильтрации предполагает прогон этих частиц через специальную систему, а затем взвешивание с помощью информации, полученной от измерения данных частиц. Полученные частицы и связанные с ними массы представляют апостериорное распределение оценочного процесса. Цикл повторяется для каждого нового измерения, и веса частиц обновляются для представления последующего распределения. Одна из основных проблем с традиционным подходом фильтрации частиц состоит в том, что в результате такой подход обычно имеет несколько частиц, имеющих очень большой вес, в отличие от большинства остальных, вес которых очень незначителен. Это приводит к нестабильности фильтрации . Эта проблема может быть решена введением частоты дискретизации, где N новых частиц берется из распределения, составленного из старых частиц. Результат оценки получают путем получения выборки среднего значения множества частиц. Если мы имеем несколько независимых выборок, то средняя выборка будет точной оценкой среднего значения, задающей конечную дисперсию.
Даже если фильтр частиц является неоптимальным, то при стремлении количества частиц к бесконечности эффективность алгоритма приближается в байесову правилу оценивания. Поэтому желательно иметь столько частиц, сколько возможно, чтобы получить наилучший результат. К сожалению, это приводит к сильному увеличению сложности вычислений, а, следовательно, вынуждает к поиску компромисса между точностью и скоростью расчета. Итак, число частиц должно быть выбрано исходя из требований к задаче оценки точности. Еще одним важным фактором для работы фильтра частиц является ограничение на частоту дискретизации. Как упоминалось ранее, частота дискретизации является важным параметром фильтрации частиц и без него в конечном итоге алгоритм становится вырождающимся. Идея заключается в том, что если веса распределяются слишком неравномерно и порог дискретизации скоро будет достигнут, то частицы с низким весом отбрасываются, и оставшееся множество образует новую вероятностную плотность, для которой могут браться новые выборки. Выбор порога частоты дискретизации представляет собой довольно сложную задачу, ведь слишком высокая частота служит причиной чрезмерной чувствительности фильтра к шуму, а слишком низкая дает большую погрешность. Также важным фактором является плотность вероятности .
В целом, алгоритм фильтрации частиц показывает хорошую производительность расчета местоположения для стационарных целей и в случае относительно медленно движущихся целей с неизвестной динамикой ускорения. В общем случае, алгоритм фильтрации частиц является более стабильным, чем расширенный фильтр Калмана, и менее склонным к вырождению и серьезным сбоям. В случаях нелинейного, негауссового распределения данный алгоритм фильтрации показывает весьма хорошую точность определения местоположения цели, в то время как алгоритм расширенной фильтрации Калмана нельзя использовать при таких условиях. К минусам данного подхода можно отнести его более высокую сложность относительно расширенного фильтра Калмана, а также то, что не всегда очевидно, как правильно подобрать параметры для этого алгоритма.
Перспективные исследования в данной области
Использование модели фильтра Калмана, подобной той, что привели мы, можно видеть в , где он используется для улучшения характеристик комплексированной системы (GPS + модель компьютерного зрения для сопоставления с географической базой), и также моделируется ситуация отказа спутникового навигационного оборудования. С помощью фильтра Калмана результаты работы системы в случае отказа были существенно улучшены (например, погрешность в определении высоты была снижена примерно в два раза, а погрешности в определении координат по разным осям снижены практически в 9 раз). Аналогичное использование фильтра Калмана приведено также в .
Интересная с точки зрения совокупности методов задача решается в . Там также используется фильтр Калмана с 5 состояниями, с некоторыми отличиями в построении модели. Полученный результат превосходит результат приведенной нами модели за счет использования дополнительных средств комплексирования (используются фото и тепловизионные изображения). Применение фильтра Калмана в данном случае позволяет уменьшить погрешность определения пространственных координат заданной точки до значения 5,5 м.
Заключение
В заключение отметим, что использование фильтра Калмана в системах определения местоположения БПЛА практикуется во многих современных разработках. Существует огромное количество вариаций и аспектов такого использования, вплоть до одновременного применения нескольких подобных фильтров с разными факторами состояний . Одним из наиболее перспективных направлений развития Калмановских фильтров видится работа над созданием модифицированного фильтра, погрешности которого будут представлены цветным шумом, что сделает его еще более ценным для решения реальных задач. Также большой интерес в данной области представляет собой частичный фильтр, с помощью которого можно фильтровать негауссовские шумы. Названное разнообразие и ощутимые результаты в повышении точности, особенно в случае отказа стандартных спутниковых навигационных систем, являются главными факторами влияния данной технологии на различные научные области, связанные с разработкой точных и отказоустойчивых навигационных систем для различных летательных аппаратов.
Рецензенты:
Лабунец В.Г., д.т.н., профессор, профессор кафедры теоретических основ радиотехники Уральского федерального университета имени первого Президента России Б.Н. Ельцина, г. Екатеринбург;
Иванов В.Э., д.т.н., профессор, зав. кафедрой технологии и средств связи Уральского федерального университета имени первого Президента России Б.Н. Ельцина, г. Екатеринбург.
Библиографическая ссылка
Гаврилов А.В. ИСПОЛЬЗОВАНИЕ ФИЛЬТРА КАЛМАНА ДЛЯ РЕШЕНИЯ ЗАДАЧ УТОЧНЕНИЯ КООРДИНАТ БПЛА // Современные проблемы науки и образования. – 2015. – № 1-1.;URL: http://science-education.ru/ru/article/view?id=19453 (дата обращения: 01.02.2020). Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
